솔직히 고백하겠습니다.
저도 주니어 시절, 데이터를 처음 다룰 때 이 문제 때문에 며칠 밤을 설친 적이 있습니다.
데이터를 산포도(Scatter plot)로 찍어보면 분명 우상향하는 예쁜 타원형인데, 막상 선형 회귀(Linear Regression)를 돌리면 결과가 이상했거든요.
우리가 눈으로 보는 '데이터의 중심축'보다 회귀선이 묘하게 눕거나 기울어져 있는 겁니다.
"라이브러리 버그인가?"
"내가 파라미터를 잘못 넣었나?"
아마 데이터 분석이나 머신러닝을 공부해보신 분들이라면 한 번쯤 느껴보셨을 당혹감일 겁니다.
최근 개발자 커뮤니티에서도 이와 관련된 아주 흥미로운 논쟁이 있었습니다.
한 개발자가 테스트 데이터를 생성하고 Least Squares(최소 제곱법)로 선을 그었는데, 선이 데이터의 중심을 관통하지 않는다는 질문이었죠.
오히려 공분산 행렬의 고유벡터(Eigenvector)를 구해서 그렸더니, 그게 훨씬 더 우리가 생각하는 '중심선'에 가까워 보인다는 겁니다.
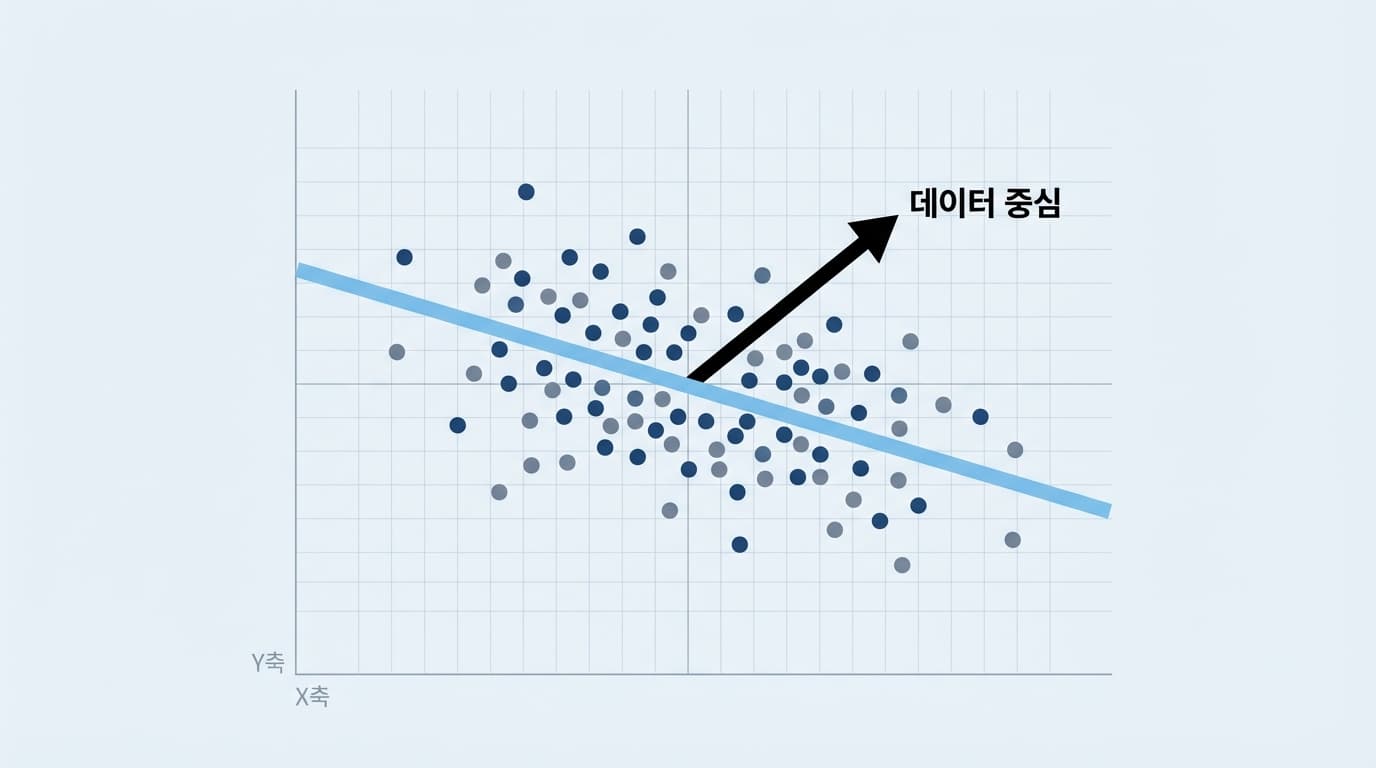
왜 이런 일이 벌어질까요?
우리의 '눈'과 '수학'이 정의하는 '거리'가 다르기 때문입니다.
이 차이를 이해하는 것이 엔지니어링 감각을 키우는 핵심입니다.
우리가 시각적으로 데이터의 중심선을 찾을 때는 무의식적으로 점과 선 사이의 최단 거리를 봅니다.
기하학적으로는 선에 수직으로 내린 발, 즉 직교 거리(Perpendicular distance)를 최소화하는 선을 찾는 것이죠.
이것이 바로 질문자가 발견한 고유벡터, 혹은 PCA(주성분 분석)나 Total Least Squares가 하는 일입니다.
데이터의 모양(Geometry) 그 자체를 요약하는 것이 목적이라면 이 방법이 맞습니다.
하지만 우리가 흔히 쓰는 OLS(Ordinary Least Squares) 회귀는 목적이 완전히 다릅니다.
회귀분석의 목표는 '데이터 요약'이 아니라 '예측'입니다.
"X라는 입력이 들어왔을 때, Y는 얼마일까?"를 맞추는 게임이죠.
그래서 OLS는 선과 점 사이의 최단 거리가 아니라, 오직 Y축 방향의 오차(Vertical distance)만을 봅니다.
X축(입력)은 정확하다고 가정하고, Y축(출력)의 오차를 최소화하는 데에만 모든 에너지를 쏟습니다.
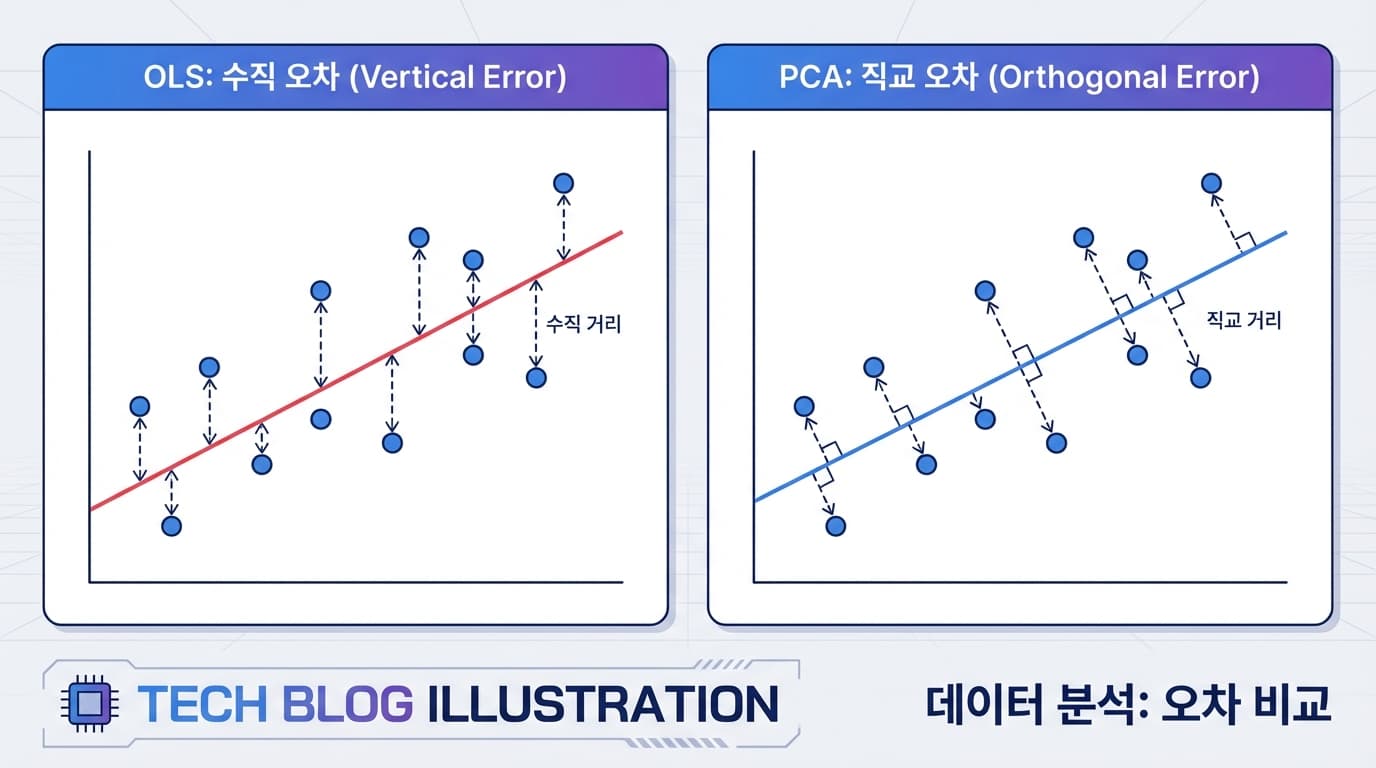
그렇기 때문에 회귀선은 시각적으로 보이는 데이터의 주축보다 항상 수평선에 가깝게 눕는 경향이 있습니다.
이것을 통계학에서는 '평균으로의 회귀(Regression to the mean)'와 관련된 현상으로 설명하기도 합니다.
여기서 우리가 얻어야 할 기술적 인사이트는 명확합니다.
도구의 목적을 정확히 파악해야 합니다.
현업에서 주니어 데이터 사이언티스트들이 종종 저지르는 실수가 있습니다.
데이터 분포가 예쁘게 나온다고 해서, 덜컥 PCA의 주축(Principal Axis)을 가져다가 예측 모델의 회귀선으로 써버리는 것입니다.
시각적으로는 그럴듯해 보일지 몰라도, 예측 성능(MSE 등)을 따져보면 결과는 참담할 수 있습니다.
예측 모델링의 관점에서는 '삐딱해 보이는' 그 회귀선이, 수학적으로는 가장 오차가 적은 최적의 해답이기 때문입니다.
반대로, 변수 간의 물리적인 관계나 기하학적 구조를 파악해야 하는 상황(예: 컴퓨터 비전의 객체 인식 등)이라면 OLS 대신 Total Least Squares를 써야 합니다.
기술은 거짓말을 하지 않습니다.
다만 우리가 그 기술이 '무엇을 최적화하고 있는지'를 오해할 뿐입니다.
여러분이 작성한 코드가 직관과 다르다고 느껴질 때, 당황하지 마십시오.
그 도구가 최소화하려는 Loss Function(손실 함수)이 무엇인지 수식을 한 번만 더 들여다보세요.
그 삐딱한 선 안에, 비즈니스가 원하는 '정확한 예측'의 비밀이 숨어있을지도 모릅니다.
